
Tích vô hướng là gì? Cách tính tích vô hướng của hai vectơ
Tích vô hướng - đây là một nội dung rất quan trọng nằm trong bộ chương trình đào tạo của bộ môn Toán lớp 10. Nắm vững cách tính tích vô hướng của hai vectơ trong mặt phẳng và các tính chất, ứng dụng sẽ giúp các bạn vượt qua các kỳ thi một cách dễ dàng hơn. Bây giờ, hãy cùng ihoc.vn khám phá các nội dung lý thuyết cũng như bài tập tính tích vô hướng 2 vecto dưới đây.
Tìm hiểu cách tính tích vô hướng của hai vectơ trong mặt phẳng
Định nghĩa tích vô hướng là gì?
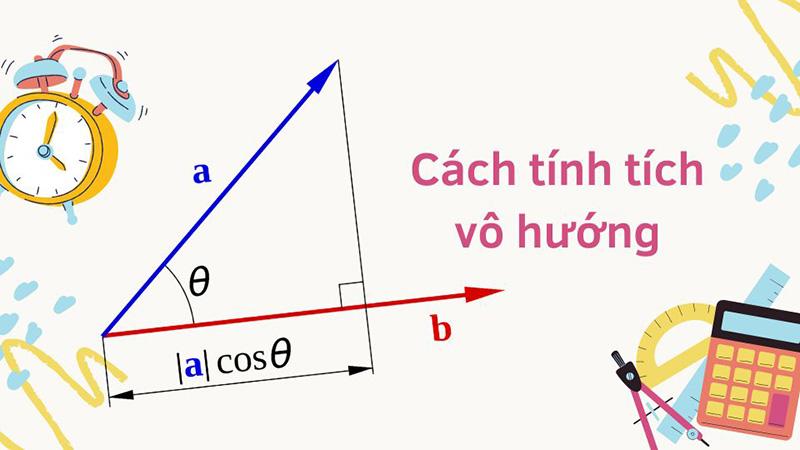
Cho hai vectơ a→ và b→ khác vectơ 0→, tích vô hướng của a→ và b→ là 1 số, được ký hiệu là a→.b→ và xác định bởi công thức sau đây: a→.b→ = |a→|.|b→| cos (a→, b→)
Trường hợp ít nhất một trong hai vectơ a→ và b→ bằng vectơ 0→, ta có quy ước như sau: a→.b→ = 0
Lưu ý:
- Nếu a→ và b→ đều khác vectơ 0→ ta có a→.b→ = 0→ ⇔ a→ ⊥ b→
- Nếu a→ = b→ thì cách tính tích vô hướng là a→. a→ (kí hiệu là a→2 được gọi là “bình phương vô hướng của vecto a”. Ta có: a→2 = |a→|. |a→| cos 0o = |a→|2
Tính chất của tích vô hướng
Với ba vectơ a→, b→, c→ bất kỳ với mọi số thực k ta có:
- a→.b→ = b→.a→ (theo tính chất giao hoán)
- a→.( b→+ c→) = a→.b→ + a→.c→ (tính chất phân phối)
- (k.a→).b→ = k.(a→,b→) = a→. (kb→)
- a→2 ≥ 0, a→2 = 0 ⇔ a→ = 0→
Từ tính chất của tích vô hướng của hai vectơ, ta có thể suy ra:
- (a→ + b→)2 = a→2 + 2a→.b→ + b→2
- (a→ - b→)2 = a→2 - 2a→.b→ + b→2
- (a→ + b→). (a→ - b→) = a→2 - b→2
Biểu thức tọa độ và ứng dụng của tích vô hướng trong mặt phẳng
Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ (O; i→; j→) cho hai vectơ a→ = (a1; a2), b→ = (b1; b2). Khi đó tích vô hướng a→ và b→ là a→.b→ = a1b1 + a2b2.
Nhận xét: Hai vectơ a→ = (a1; a2), b→ = (b1; b2) khác vectơ 0→ vuông góc với nhau ⇔ a1b1 + a2b2 = 0
Ứng dụng công thức
- Độ dài của vectơ: Độ dài của vectơ a→ = (a1; a2) được tính theo công thức:

- Góc giữa hai vectơ: Từ định nghĩa tích vô hướng của hai vectơ trong mặt phẳng, suy ra nếu a→ = (a1; a2), b→ = (b1; b2) khác vectơ 0→ thì:
- Khoảng cách giữa hai điểm: Khoảng cách giữa hai điểm A (xA, yA), B (xB, yB) được tính theo công thức sau:
Sơ đồ tư duy công thức tích vô hướng
- Có thể bạn quan tâm: Cách học giỏi môn toán? 8 Bí thuật làm chủ toán học
Bài tập tính tích vô hướng của 2 vecto trong mặt phẳng
Dạng 1: Chứng minh hai vectơ vuông góc bằng cách tính tích vô hướng của hai vectơ
- Phương pháp 1: Sử dụng định nghĩa nếu (a→, b→) = 90o thì a→ ⊥ b→
- Phương pháp 2: Sử dụng tính chất tích vô hướng và áp dụng trong hệ tọa độ a→ = (x;y), b→ = (x’;y’) ⇔ a→ ⊥ b→ và xx’ + yy’ = 0
Ví dụ 1: Cho hai vectơ a→ và b→ vuông góc với nhau và |a→| = 1; |b→| = √2. Chứng minh hai vectơ 2a→ - b→ và a→ + b→ vuông góc với nhau.
Bài giải:

Ví dụ 2: Cho tam giác ABC vuông tại A, biết AB = a, AC = 2a. Gọi M là trung điểm của BC và điểm D bất kỳ thuộc AC. Tính AD theo a để BD AM.
Bài Giải:

Dạng 2: Tìm m để góc giữa hai vectơ bằng 1 số đo cho trước (45 độ, góc tù, góc nhọn)
Phương pháp giải:
- B1: Xác định vectơ (nếu chưa có) theo ẩn m
- B2: Tính độ dài các vectơ theo ẩn m
- B3: Áp dụng công thức tính cos góc giữa hai vectơ
- B4: Đưa ra phương trình chứa ẩn m, góc giữa hai vectơ bằng α = cos (a→, b→) = cos α B5: Giải phương trình, đưa ra giá trị của m.
Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho hai vectơ a→ = (3;m) và b→ = (1;7). Xác định m để (a→, b→) = 45 độ. Bài Giải: Ta có:

Tích vô hướng và tích có hướng là hai dạng bài tập Toán không thể thiếu khi học THPT. Hãy cùng ghi chú lại những nội dung về cách tính tích vô hướng vào sổ tay. Cùng với đó là sự luyện tập nhiều lần để đem đến thành tích tốt trong các kỳ thi sắp tới nhé.
Link nội dung: https://cmp.edu.vn/cach-tinh-tich-vo-huong-cua-hai-vecto-a52487.html