a) ∆ là trục trước sau, ta tách nút K thành K1, K2 như sau:
Mạch điện tương đương:
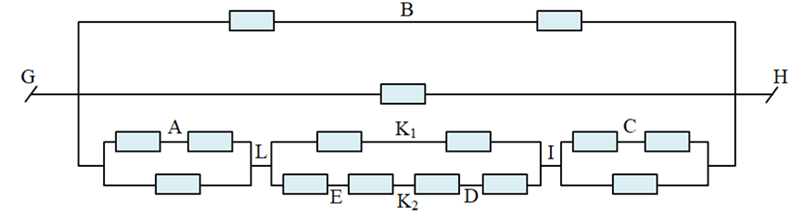
Điện trở tương đương:
(begin{array}{l}{R_{GL}} = {R_{IH}} = dfrac{{2R.R}}{{2R + R}} = dfrac{{2R}}{3}{R_{LI}} = dfrac{{2R.4R}}{{2R + 4R}} = dfrac{{4R}}{3} Rightarrow {R_{GLIH}} = dfrac{{2R}}{3} + dfrac{{4R}}{3} + dfrac{{2R}}{3} = dfrac{{8R}}{3}dfrac{1}{{{R_{GH}}}} = dfrac{1}{{2R}} + dfrac{1}{R} + dfrac{3}{{8R}} = dfrac{{15}}{{8R}} Rightarrow {R_{GH}} = dfrac{{8R}}{{15}} = dfrac{{8.10}}{{15}} = dfrac{{16}}{3},,left( Omega right)end{array})
b) ∆ là trục trước sau, ta tách nút K thành K1, K2 như sau:
Mạch điện tương đương:
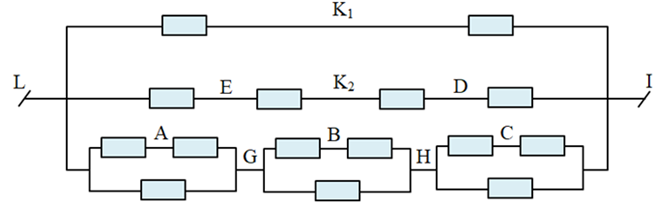
Điện trở tương đương:
(begin{array}{l}{R_{LG}} = {R_{GH}} = {R_{HI}} = dfrac{{2R.R}}{{2R + R}} = dfrac{{2R}}{3}{R_{LGHI}} = 3.dfrac{{2R}}{3} = 2Rdfrac{1}{{{R_{LI}}}} = dfrac{1}{{2R}} + dfrac{1}{{4R}} + dfrac{1}{{2R}} = dfrac{5}{{4R}} Rightarrow {R_{LI}} = dfrac{{4R}}{5} = dfrac{{4.10}}{5} = 8,,left( Omega right)end{array})
c) ∆ là trục trước sau, ta tách nút L thành L1, L2 như sau:
Mạch điện tương đương:
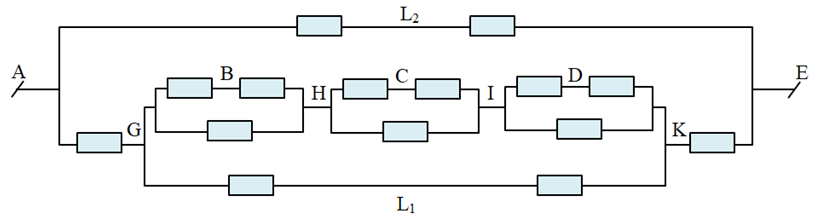
Điện trở tương đương:
(begin{array}{l}{R_{GH}} = {R_{HI}} = {R_{IK}} = dfrac{{2R.R}}{{2R + R}} = dfrac{{2R}}{3}{R_{GHIK}} = 3.dfrac{{2R}}{3} = 2R{R_{GK}} = dfrac{{2R}}{2} = R{R_{AGKE}} = 3Rdfrac{1}{{{R_{AE}}}} = dfrac{1}{{2R}} + dfrac{1}{{3R}} = dfrac{5}{{6R}} Rightarrow {R_{AE}} = dfrac{{6R}}{5} = dfrac{{6.10}}{5} = 12,,left( Omega right)end{array})
d) Cách 1: Phương pháp chập điểm:
AI là trục đối xứng, chập các điểm sau:
- L và G.
- E và B.
- H và K.
- C và D.
Ta có mạch điện tương đương:
Điện trở tương đương:
(begin{array}{l}{R_{AL}} = dfrac{R}{2}{R_{LH}} = {R_{HI}} = dfrac{{left( {dfrac{R}{2} + dfrac{R}{2}} right).dfrac{R}{2}}}{{dfrac{R}{2} + dfrac{R}{2} + dfrac{R}{2}}} = dfrac{R}{3} Rightarrow {R_{AI}} = {R_{AL}} + {R_{LH}} + {R_{HI}} = dfrac{R}{2} + dfrac{R}{3} + dfrac{R}{3} = dfrac{{7R}}{6}end{array})
Cách 2: Phương pháp bỏ điện trở
AI là trục đối xứng, ta có thể bỏ được điện trở LG, ta có:
Ta có mạch điện tương đương:

Điện trở tương đương:
(begin{array}{l}{R_{AL}} = dfrac{R}{2}{R_{LH}} = {R_{HI}} = {R_{LK}} = {R_{KI}} = dfrac{{2R.R}}{{2R + R}} = dfrac{{2R}}{3}{R_{LI}} = dfrac{{left( {2.dfrac{{2R}}{3}} right).left( {2.dfrac{{2R}}{3}} right)}}{{left( {2.dfrac{{2R}}{3}} right) + left( {2.dfrac{{2R}}{3}} right)}} = dfrac{{2R}}{3} Rightarrow {R_{AI}} = {R_{AL}} + {R_{LI}} = dfrac{R}{2} + dfrac{{2R}}{3} = dfrac{{7R}}{6} = dfrac{{7.10}}{6} = dfrac{{35}}{3},,left( Omega right)end{array})


